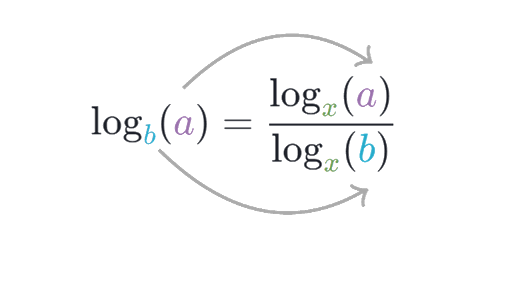Student Success Commons: MAT 127: College Algebra

Linear equations are vital in many real-world scenarios. For instance, you're in this class right now, in the real world, and you have to learn about linear equations.

Algebraic properties are rules that describe the relationships between numbers and variables in algebraic expressions and equations. These properties allow you to manipulate and solve equations.

When two numbers are added, the sum is the same regardless of the order in which the numbers are added. Example: 2 + 3 is the same as 3 + 2.

When three or more numbers are added, the sum is the same regardless of the way in which the numbers are grouped. Example: (6 + 3) + 2 is the same as 6 + (3 + 2).

When two numbers are multiplied together, the product is the same regardless of the order in which the numbers are multiplied. Example: 3 • 5 is the same as 5 • 3 .

When three or more numbers are multiplied, the product is the same regardless of the way in which the numbers are grouped. Example: (2 • 5) • 7 is the same as 2 • (5 • 7) .

The sum of two numbers times a third number is equal to the sum of each addend times the third number. Example: 5(7 + 2) = 45 equals 5 • 7 + 5 • 2 = 45

Adding 0 to any number does not change the original value. Example: -65 + 0 = -65

Multiplying any number by 1 does not change the original value. Example: -65(1) = -65.

Remember: the number 1 can be written as a fraction wherein the numerator and denominator are the same. For example, 5/5, -6/-6, and 43/43 are all equivalent to 1. This fact can come in handy when working with problems involving fractions.

In algebra, the number 1 is often implied rather than explicitly written because of this property. When a variable is written alone, for example, x, it's understood to be equal to 1x. We will often leave the coefficient 1 out to simplify our work.

The sum of any number and its additive inverse is equal to 0. Example: 73 + -73 = 0

The product of any number and its reciprocal is equal to 1. Example: (4/5)(5/4) = 1

Any number multiplied by 0 is equal to 0. Example: 0(1/3) = 0

To solve linear equations, follow these basic steps (and don't forget about the properties shown above!):

1. Simplify both sides:
   • Remove parentheses using the distributive property.
   • Combine like terms on each side of the equation.
2. Use addition or subtraction to move all variable terms to one side and constant terms to the other.
3. Solve for the variable:
   • Use multiplication or division to isolate the variable completely.
4. Check your solution:
   • Substitute the value you found for the variable back into the original equation to verify that it makes the equation true.

CH 1.1 EXAMPLES:

Solve the following equations for “x”:

1. 5x + 2 = 4

2. 2(x – 3) + 7 = 0

3. 2x + 3 = 4x - 7

SOLUTIONS:

1. 5x + 2 = 4

      5x = 2

        x = 2/5

The solution set it {2/5}

2. 2(x – 3) + 7 = 0

  2x – 6 + 7 = 0

        2x + 1 = 0

     2x = -1

                x = -½

The solution set is {-½}

3. 2x + 3 = 4x – 7

      10 = 2x

        x = 5

The solution set is {5}

Additional resources:

• How To Solve Linear Equations In Algebra (The Organic Chemistry Tutor)
• Linear equations 1 (Khan Academy)
• Linear equations 2 (Khan Academy)
• Linear equations 3 (Khan Academy)
• Linear equations 4 (Khan Academy)
• Why Dividing by 0 is Undefined

Why have an equation if not to solve it?

Five steps for problem solving:

1. Read the problem carefully and identify what is being asked. Try to express the problem in your own words to ensure comprehension.
2. Assign a variable to represent the unknown value. "x" is one of the most commonly used placeholders used in mathematics, but you can use any variable that makes sense to you as long as you clearly label your variable and its meaning.
3. Write an equation.
4. Solve the equation. Use the properties of algebra to isolate the variable.
5. State and evaluate the answer. Ask yourself if it makes sense in context. Does it answer the original question? If yes, you're done. If not, review these steps and try again.

CH 1.2 EXAMPLES:

1. How many liters of 30% alcohol solution and 80% alcohol solution must be mixed to obtain 40L of 50% alcohol solution?

2. Marley and Jane both run a 200m race. If Jane is 1.2 times as fast as Marley, and it takes Jane 21 seconds to complete the race, how long does it take Marley?

SOLUTIONS:

1. How many liters of 30% alcohol solution and 80% alcohol solution must be mixed to obtain 40L of 50% alcohol solution?

Let “x” represent the liters of the 30% alcohol solution:

0.30x + 0.80(40 – x) = 0.50(40)

  0.30x + 32 – 0.80x = 20

                     -0.50x = -12

                             x = 24

24L of the 30% alcohol solution must be mixed with 40 – 24 = 16L of the 80% alcohol solution to obtain 40L of 50% alcohol solution.

2. Marley and Jane both run a 200m race. If Jane is 1.2 times as fast as Marley, and it takes Jane 21 seconds to complete the race, how long does it take Marley?

Let “M” represent Marley’s speed. Remember that if d = rt, then r = d/t. Jane’s rate of speed therefore is 200/21.

Since Jane is 1.2 times as fast as Marley, 200/21 is 1.2 times Marley’s speed: 200/21 = 1.2M

Solve for M:

200/(21 ⋅ 1.2) = M

     200/(25.2) = M

Recall that this is in d/t format. Therefore, it takes Marley 25.2 seconds to run the 200m race.

Additional resources:

• Example: working through a word problem (Khan Academy)
• Example: working through a word problem (Khan Academy)
• Distance, rate, time word problem

Once upon a time mathematicians realized you couldn't take the square root of a negative number. This was a total bummer because that left a lot of problems unsolved. But then Girolamo Cardano was like, "Bro, look, we can do this thing and it will work."  And René Descartes said, "What are you going to do, make something up? Oooh look at my 'iMaGiNaRy' numbers." But Cardano was just like "Yep." And Descartes was like, "... Okay fine, I'll go with it but I'm not happy about it," and now we have the imaginary unit.*

_{*Some liberties were taken in the writing of this historical account. But if you're interested in the full story, visit the SSC library to learn more!}

The imaginary unit, denoted by the lowercase letter "i," is equal to the square root of negative 1. It was initially a theoretical concept, considered "imaginary" because no real number could be squared to result in a negative number. However, it became crucial for solving certain polynomial equations and formed the basis for the development of complex numbers.

To simplify i^x determine the closest value less than or equal to x that is divisible by 4. Perform the division and focus on the remainder:

• If the remainder is 3 then the solution is –i;
• if the remainder is 2 then the solution is –1;
• if the remainder is 1 then the solution is i;
• if the remainder is 0 then the solution is 1

Click image to enlarge.

CH 1.3 EXAMPLES:

Simplify the following:

1. √(-4)
2. √(-12)
3. (2 + 3i) - (3 – 5i)
4. i⁹⁷

SOLUTIONS:

1. √(-4) = i√(4) = 2i
2. √(-12) = i√(12) = i√(4)√(3) = 2i√(3)
3. (2 + 3i) - (3 – 5i) = -1 + 8i
4. i^{97 =} i⁹⁶i¹ = i

Additional resources:

• Imaginary numbers - basic introduction (The Organic Chemistry Tutor on YouTube)
• Imaginary numbers explained in 60 seconds or less
• A brief history of "i"
• Powers of imaginary units (Khan Academy article)

"There is nothing in the world quite so satisfying as a quadratic equation." — said somebody, probably, at some point.

The zero-factor property states that if ab = 0 then a or b or both = 0.

The square root property states that the solution set of x² = k is ±√k

There are three main methods to solve quadratic equations:

1. Factoring: This method involves rewriting the quadratic expression as a product of two linear expressions. Does not work if the quadratic equation isn’t easily factorable. Note the following generic patterns:
   • ax² + bx + c = 0 -----> (x + ?)(x + ?) All terms positive.
   • ax² - bx - c = 0 -----> (x - ?)(x + ?) When all terms are negative, one factor will be negative, and one will be positive.
   • ax² + bx - c = 0 -----> (x + ?)(x - ?) When b is positive and c is negative, one factor will be positive and the other will be negative.
   • ax² - bx + c = 0 -----> (x - ?)(x - ?) When b is negative and c is positive, both factors will be negative
2. Completing the Square: This method involves manipulating the quadratic equation to create a perfect square trinomial on one side. This method will always work.
3. Quadratic Formula: This formula provides a direct solution for any quadratic equation in the form ax² + bx + c = 0. This method will always work.

Rationalizing the denominator means rewriting a fraction so that the denominator is a rational number, meaning it doesn't contain any radicals. Though a denominator can be complex, it is common to want to avoid complex numbers in the denominator. You can then simplify the fraction to remove "i" from the denominator by multiplying the numerator and denominator by the complex conjugate of the denominator.

When using the quadratic formula, the discriminant (b² - 4ac) indicates how many solutions and what type. See the table below:

The multiplicity of a root (also known as a zero) of a polynomial is the number of times the corresponding factor appears in the factored form of the polynomial. For example, in the polynomial (x - 2)³ (x + 1)², the root x = 2 has a multiplicity of 3, and the root x = -1 has a multiplicity of 2. This will be discussed more in chapter 3.

Additional resources:

• Solving a quadratic equation using all 3 methods
• Rationalizing the denominator - examples and explanation
• How to: Completing the square
• Quadratic formula solver

You weren't expecting geometry, were you?

Additional resources:

• 4 various examples - perfect for practice!
• How to use the Pythagorean Theorem to determine if 3 points form a right triangle

Is that boss level music?

PARTS OF A RADICAL:

Additional resources:

• Linear and rational equation practice problems
• Work rate practice problems

Things don't always balance out. But it's okay, we have math for that.

Important!

When multiplying or dividing both sides of an inequality by a negative you must reverse the inequality symbol.

Additional resources:

• All about inequalities (excellent article!)

This is the |absolute| best. Ba dum tss.

The mathematical way to know exactly where you are.

Suppose that P(x₁, y₁) and Q(x₂, y₂) are two points in a coordinate plane. The distance between points P and Q, written d(P, Q), is given by the following formula: 

The coordinates of the midpoint, M, of the line segment with endpoints P(x₁, y₁) and Q(x₂, y₂) are given by the following formula: 

No dysfunctional relationships here, no way...

I really have nothing pithy to say about this.

The slope, m, of the line through the points (x₁, y₁) and (x₂, y₂) is given by the following:


Note: the slope of a vertical line is undefined. The slope of a horizontal line is 0.

You probably thought this chapter couldn't possibly get more exciting but oh ho ho...you might be right.

Some models are just so beautiful, am I right?

A parabola ("per-AH-boh-luh") is a U-shaped curve, the graphical representation of a quadratic function, characterized by several key features including:

• Vertex: The point where the parabola changes direction, either reaching a maximum or minimum value. The vertex is represented by the point (h, k). (See "QUADRATIC EQUATION IN VERTEX FORM as well as the additional resources available for this section for more information about "h" and "k".)
• Axis of Symmetry: A vertical line that passes through the vertex and divides the parabola into two symmetrical halves.
• y-intercept: The point where the parabola crosses the y-axis.
• x-intercept: The point(s) where the parabola crosses the x-axis, if it crosses.

Quadratic equation transformations involve changing the simplest quadratic function, F(x) = x², by applying different operations (see image, click to enlarge or download).

Additional resources

• How To Find The Vertex of a Parabola (three different ways) (The Organic Chemistry Tutor)

Like synthetic cheese.

Additional resources:

• Long Division with Polynomials (The Organic Chemistry Tutor)
• Beginner's Guide to Synthetic Division
• Synthetic Division intro Example by Khan Academy
• Synthetic Division

Here the zeros are the heroes.

Additional resources:

• Intro to Zeros (video)
• Rational Zero Theorem Tested (video)
• Finding All the Zeros of a Polynomial (video)
• Finding Zeros of Polynomial Functions (article)
• Online Zeros Calculator (calculator)

I bet your excitement is like f(x) = a^x where a < 0.

An exponential function calculates the exponential growth or decay of data. The basic exponential function is f(x) = a^x, where x is the input variable as an exponent, and a is a positive number greater than 1.

Note: Exponential functions are useful for modeling real-world phenomena like populations, radioactive decay, interest rates, and the amount of medicine in the bloodstream!

The word "logarithm" originates from the Greek words "logos" (meaning "proportion" or "ratio") and "arithmos" (meaning "number"). John Napier coined the term in the early 17th century. So now we both know.

Logarithms are a way of writing and working with the exponents. A logarithm is the power to which a number must be raised in order to get some other number For example log₃ 9= 2, because 3 must be raised to the power of 2 to in order to equal 9.

If a > 0, a  ≠ 1, and x > 1 then the logarithmic function with base a is as follows: 

Log_ax = n 

Read as "Log base a of x equals n."

Where "a" is the base, "x" is the argument (also called the answer), and "n" is the exponent. 

The following table shows several pairs of equivalent statements:

Properties of Logarithms

For x > 0, y > 0, a > 0, a ≠ 1, and "r" is any real number:

• PRODUCT PROPERTY: log_axy = log_ax + log_ay
• QUOTIENT PROPERTY: log_ax/y = log_ax - log_ay
• POWER PROPERTY: log_ax^r = r log_ax
• LOGARITHM OF 1: log_a1 = 0
• BASE a OF LOGARITHM a: log_aa = 1

Theorem on Inverses

For a > 0, a ≠ 1, the following properties hold:

a^log_ax = x (for x > 0)   and   log_aa^x = x

Additional resources:

• Intro to logarithms (video)
• Logarithms—Definitions, rules, examples (article)

Ah yes, look at this field of fresh, natural logarithms, just about ripe for the harvest.

The two most important bases for logarithms are base 10 and base e. Base 10 logarithms are called common logarithms. The common logarithm of x is written log x where the base is understood to be 10. Basically, is you seem something like log 2 or log 9, it is implied that the base is 10.

log x = log₁₀x

Logarithms with base e are called natural logarithms and are written as ln x (pronounced "L n x" or "El-en x"). They're called natural logarithms because they occur in natural situations that involve growth or decay.

ln x = ln_ex

Recall that "e" represents a fundamental constant, often referred to as Euler's number, and is approximately equal to 2.71828. It's the limit of the expression (1 + 1/n)ⁿ as n approaches infinity. (You'll learn more about limits if you study calculus.)

Many calculators only have log and ln built in, making logarithms with other bases difficult to calculate. However, the change of base theorem is useful for evaluating logarithms where the base is something other than 10 or e. For any positive, real numbers x, a, and b where neither a nor b = 1, the following is true:

For example, to calculate log₇21 you can use the change of base theorem and compute the following:

This is just like the last section except different.

Property of Logarithms:

If x > 0, y > 0, a > 0, and a ≠ 1, then the following holds:

x = y is equivalent to log_ax = log_ay

Additional resources:

• How to Solve Logarithmic Equations - Simple and Easy Method (video)
• Solving Logarithmic Equations (video)

After finishing this section, please go back and laugh at my 4.2 joke.

In many situations in ecology, biology, economics, and the social sciences, a quantity (y) changes at a rate proportional to the amount present (y₀). The amount present at time t is a special function of t called an exponential growth or decay function:

Let y₀ be the amount or number present at  time t = 0. Then, under certain conditions, the amount y present at any time t is modeled by 

y = y₀e^kt, where k is a constant

The constant k determines the type of function. When k > 0, the function describes growth. When k < 0, the function describes decay.

A system of linear equations is a set of two or more linear equations that involve the same variables. For example 2x + 3y = 15 and x - 2y = 7 are both linear equations with two variables (x and y). When considered together, they form a system of linear equations.

Additional resources:

• Solving systems of linear equations