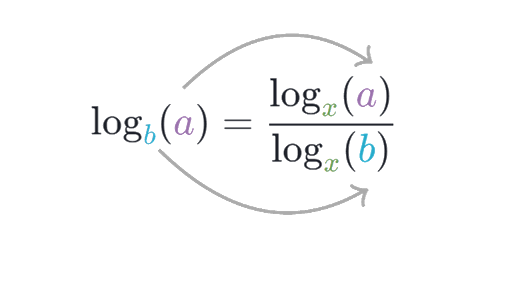Skip to Main Content SSC banner SSC banner

Student Success Commons: MAT 127: College Algebra

College Algebra Resources

PAGE UNDER CONSTRUCTION. CHECK BACK SOON FOR MORE RESOURCES.

 

Please keep in mind that any notes, videos, and calculators provided on this page are no substitute for attending class. These resources are here to supplement the information from your instructor and textbook. First and foremost please be sure to follow any directions and use any resources your teacher provides.

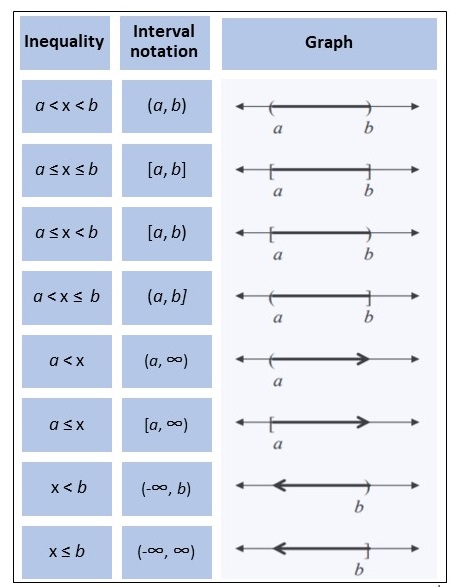
REVIEW

Keep these basics of arithmetic and algebra in mind as you take your college algebra class. If you want to review any of these concepts just click on the link to be taken to an external learning resource.

CHAPTER 1

Image courtesy of Statistics How To

CHAPTER 2

CHAPTER 3

Chapter 3.3

The zeros of a polynomial are the x-values that, when plugged in, make the polynomial equal to zero. Several theorems exist to aid in finding all the zeros of a polynomial:

1. Fundamental Theorem of Algebra:
  • Statement: Every polynomial of degree n (where n > 0) has at least one complex zero.
  • Implication: A polynomial of degree n has exactly n complex zeros, counting multiplicities (some zeros might be repeated; see definition of "Multiplicity" later in these notes). 
2. Factor Theorem:

  • Statement:

    If k is a zero of a polynomial f(x), then (x - k) is a factor of f(x), and vice versa.

  • Use:

    If you find a zero, you can use it to factor the polynomial and find other zeros. 

3. Rational Zero Theorem:

  • Statement:

    If a polynomial f(x) with integer coefficients has a rational zero p/q (where p and q are integers with no common factors), then p must be a factor of the constant term of f(x), and q must be a factor of the leading coefficient.

  • Use:

    Helps identify possible rational zeros to test using synthetic division or direct substitution. This is often a good place to start.

4. Remainder Theorem:
  • Statement: If a polynomial f(x) is divided by (x - k), then the remainder is f(k). 
  • Use: If f(k) = 0, then k is a zero of f(x), and (x - k) is a factor. 
5. Upper and Lower Bounds Theorem:
  • Statement: If c > 0 and all the coefficients in the quotient and remainder are non-negative when dividing f(x) by (x - c), then c is an upper bound for the real zeros of f(x). If c < 0 and the coefficients in the quotient and remainder alternate signs, then c is a lower bound.
  • Use: Helps narrow down the range of possible real zeros. 
6. Conjugate Zeros Theorem:

  • Statement:

    If a polynomial with real coefficients has a complex zero a + bi, then its complex conjugate a - bi is also a zero.

  • Use:

    Helps identify all zeros, including complex ones, if you know one complex zero. 

 

The multiplicity of a zero refers to the number of times a factor appears in the fully factored form of the polynomial. For example, if (x-a) appears twice in the factored form, then 'a' is a zero with a multiplicity of 2. 

 

Check out the following resources for more support:

CHAPTER 4

Chapter 4.1

A one-to-one function is a function where each input maps to a unique output, meaning no two different inputs produce the same output. The horizontal line test is useful, visual way to determine if a function is or isn't one-to-one. Looking at the graph of f(x), if any horizontal line intersects the graph of the function at more than one point, then the function is not one-to-one. (See "Horizontal Line Test and One-to-One Functions" video on YouTube.)

Inverse functions reverse the inputs and outputs of a function. That is, when you put an x value into the original function and get a y value, you can put that y value into the inverse function and get the original x value back. Note that not all functions have inverses; only functions that are one-to-one do, see below for more info. The notation for an inverse function "f-1" (read as "f inverse"), where "f" represents the original function; meaning if you have a function named "f", its inverse would be written as f-1. Keep in mind that the " -1 " does not represent an exponent, but rather signifies the inverse operation.

To find an inverse function:

  1. Ensure the function is one-to-one
  2. Replace f(x) with y so as to have an equation that begins "y = "
  3. Swap x and y
  4. Solve for y
  5. Replace y with f-1  

For example:

original equation:

f(x) = x + 5

replace f(x) with y:

y = x + 5

swap x and y:

x = y + 5

solve for y:

y = x - 5

replace y with f-1(x): 

f-1(x) = x - 5

You can verify one function is the inverse of another by using composition:

If f is one-to-one then g is the inverse of f if:

(f ○ g)(x) = x for every x in the domain of g

(g ○ f )(x) = x for every x in the domain of f

 

Check out the following resources for more support:

Chapter 4.2

An exponential function calculates the exponential growth or decay of data. The basic exponential function is f(x) = ax, where x is the input variable as an exponent, and a is a positive number greater than 1.

Note: Exponential functions are useful for modeling real-world phenomena like populations, radioactive decay, interest rates, and the amount of medicine in the bloodstream!

CHARACTERISTICS OF THE GRAPH f(x) = ax
The points (-1, 1/a) and (0,1) and (1,a) are on the graph.

If a is greater than 1, then f is an increasing function. On the other hand, if a is less than 1 but greater than 0, f is a decreasing function.

a > 0 → increasing

0 < a < 1 → decreasing
The x-axis is the horizontal asymptote.
The domain is (-∞, ∞), and the range is (0, ∞)

 

Chapter 4.3

Logarithms are a way of writing and working with the exponents. A logarithm is the power to which a number must be raised in order to get some other number For example log3 9= 2, because 3 must be raised to the power of 2 to in order to equal 9.

The general form is as follows: 

Logbx = n 

Read as "Log base b of x equals n."

Where "b" is the base, "x" is the argument (also called the answer), and "n" is the exponent. 

 

The following table shows several pairs of equivalent statements:

EXPONENTIAL FORM LOGARITHMIC FORM
23 = 8 log28 = 3
102 = 100 log10100 = 2
51 = 5 log55 = 1
3-2 = 1/9 log31/9= -2
0.5-4 = 16 log0.516 = -4

Check out the following resources for more support:

The two most important bases for logarithms are base 10 and base e. Base 10 logarithms are called common logarithms. The common logarithm of x is written log x where the base is understood to be 10. Basically, is you seem something like log 2 or log 9, it is implied that the base is 10.

log x = log10x

Logarithms with base e are called natural logarithms and are written as ln x (pronounced "L n x" or "El-en x"). They're called natural logarithms because they occur in natural situations that involve growth or decay.

ln x = lnex

 

Recall that "e" represents a fundamental constant, often referred to as Euler's number, and is approximately equal to 2.71828. It's the limit of the expression (1 + 1/n)n as n approaches infinity. (You'll learn more about limits if you study calculus.)

Many calculators only have log and ln built in, making logarithms with other bases difficult to calculate. However, the change of base theorem is useful for evaluating logarithms where the base is something other than 10 or e. For any positive, real numbers x, a, and b where neither a nor b = 1, the following is true:

For example, to calculate log721 you can use the change of base theorem and compute the following:

CHAPTER 5

A system of linear equations is a collection of two or more linear equations involving the same variables. For example 2x + 3y = 15 and x - 2y = 7 are both linear equations with two variables (x and y). When considered together, they form a system of linear equations. 

 

Check out the following resources for more support:

 

 

 

Student Success Commons at York County Community College

112 College Drive Wells, ME 04090
Room 201
ycccssc@mainecc.edu
207-216-4300


  

Quick links:  YCCC Homepage  |  MyYCCC Portal  |  Library  |  YCCC Email  |   Brightspace  |  Technical Support