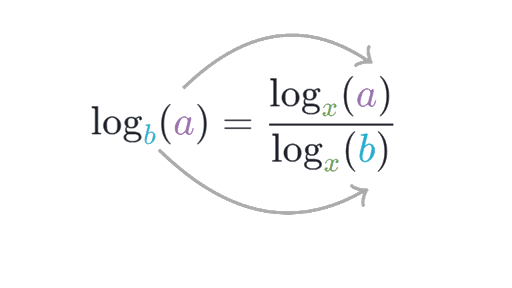Any YCCC student enrolled in a math (MAT) class or taking a course that involves math—yes, even if it’s just entering a crazy formula in Microsoft Excel!
Math tutoring covers any MAT course as well as support for any student using Microsoft Excel to perform calculations. Tutoring for dosage calculations is also available with Karissa Cole.
Please note: classes coded as ACC, BUS, and FIN are not specifically covered under Student Success Commons math tutoring. Math tutors will help the best we can, but if you need support with any of these classes please reach out to your instructor and student success coach.
Please keep in mind that any notes, videos, and calculators provided on this page are no substitute for attending class. These resources are here to supplement the information from your instructor and textbook. First and foremost please be sure to follow any directions and use any resources your teacher provides.
REVIEW RESOURCES
Keep these basics of arithmetic and algebra in mind as you take your college algebra class. If you want to review any of these concepts just click on the link to be taken to an external learning resource.
- Sets
- Real numbers and their properties
- Order of operations
- Absolute value
- FOILing
- Factoring polynomials
- Roots and radicals (note: this is discussed more in chapters 1 and 4)
Chapter 1: Equations and Inequalities
Equations keep the math world balanced, and inequalities show us when it’s not — college algebra teaches both so you can solve problems whether life is fair or not! Use the numbered tabs above to find helpful notes, formulas, and additional resources for each section of this chapter.
Linear equations are vital in many real-world scenarios. For instance, you're in this class right now, in the real world, and you have to learn about linear equations.
Algebraic properties are rules that describe the relationships between numbers and variables in algebraic expressions and equations. These properties allow you to manipulate and solve equations.
When two numbers are added, the sum is the same regardless of the order in which the numbers are added. Example: 2 + 3 is the same as 3 + 2.
When three or more numbers are added, the sum is the same regardless of the way in which the numbers are grouped. Example: (6 + 3) + 2 is the same as 6 + (3 + 2).
When two numbers are multiplied together, the product is the same regardless of the order in which the numbers are multiplied. Example: 3 • 5 is the same as 5 • 3 .
When three or more numbers are multiplied, the product is the same regardless of the way in which the numbers are grouped. Example: (2 • 5) • 7 is the same as 2 • (5 • 7) .
The sum of two numbers times a third number is equal to the sum of each addend times the third number. Example: 5(7 + 2) = 45 equals 5 • 7 + 5 • 2 = 45
Adding 0 to any number does not change the original value. Example: -65 + 0 = -65
Multiplying any number by 1 does not change the original value. Example: -65(1) = -65.
Remember: the number 1 can be written as a fraction wherein the numerator and denominator are the same. For example, 5/5, -6/-6, and 43/43 are all equivalent to 1. This fact can come in handy when working with problems involving fractions.
In algebra, the number 1 is often implied rather than explicitly written because of this property. When a variable is written alone, for example, x, it's understood to be equal to 1x. We will often leave the coefficient 1 out to simplify our work.
The sum of any number and its additive inverse is equal to 0. Example: 73 + -73 = 0
The product of any number and its reciprocal is equal to 1. Example: (4/5)(5/4) = 1
Any number multiplied by 0 is equal to 0. Example: 0(1/3) = 0
To solve linear equations, follow these basic steps (and don't forget about the properties shown above!):
- Simplify both sides:
- Remove parentheses using the distributive property.
- Combine like terms on each side of the equation.
- Use addition or subtraction to move all variable terms to one side and constant terms to the other.
- Solve for the variable:
- Use multiplication or division to isolate the variable completely.
- Check your solution:
- Substitute the value you found for the variable back into the original equation to verify that it makes the equation true.
If solving the equation leads to a single solution is conditional. Its solution set consists of a single element.
If solving the equation leads to a false statement the equation is a contradiction. As there is no solution, the solution set is ∅
CH 1.1 EXAMPLES:
Solve the following equations for “x”:
- 5x + 2 = 4
- 2(x – 3) + 7 = 0
- 2x + 3 = 4x - 7
SOLUTIONS:
- 5x + 2 = 4
5x = 2
x = 2/5
The solution set it {2/5}
- 2(x – 3) + 7 = 0
2x – 6 + 7 = 0
2x + 1 = 0
2x = -1
x = -½
The solution set is {-½}
- 2x + 3 = 4x – 7
10 = 2x
x = 5
The solution set is {5}
Additional resources:
Why have an equation if not to solve it?
Five steps for problem solving:
- Read the problem carefully and identify what is being asked. Try to express the problem in your own words to ensure comprehension.
- Assign a variable to represent the unknown value. "x" is one of the most commonly used placeholders used in mathematics, but you can use any variable that makes sense to you as long as you clearly label your variable and its meaning.
- Write an equation.
- Solve the equation. Use the properties of algebra to isolate the variable.
- State and evaluate the answer. Ask yourself if it makes sense in context. Does it answer the original question? If yes, you're done. If not, review these steps and try again.
- Simple Interest:
I = PRT, where I = interest, P = principal, R = interest rate, and T = time. - Distance-Rate-Time:
d = rt, where d = distance, r = rate (speed), and t = time. - Cost Function:
C(x) = mx + b, where C(x) = total cost, x = number of units, m = cost per unit, and b = fixed cost. - Linear Equations in Mixture Problems: Determining the amount of each substance needed to achieve a desired mixture.
CH 1.2 EXAMPLES:
- How many liters of 30% alcohol solution and 80% alcohol solution must be mixed to obtain 40L of 50% alcohol solution?
- Marley and Jane both run a 200m race. If Jane is 1.2 times as fast as Marley, and it takes Jane 21 seconds to complete the race, how long does it take Marley?
SOLUTIONS:
- How many liters of 30% alcohol solution and 80% alcohol solution must be mixed to obtain 40L of 50% alcohol solution?
Let “x” represent the liters of the 30% alcohol solution:
0.30x + 0.80(40 – x) = 0.50(40)
0.30x + 32 – 0.80x = 20
-0.50x = -12
x = 24
24L of the 30% alcohol solution must be mixed with 40 – 24 = 16L of the 80% alcohol solution to obtain 40L of 50% alcohol solution.
- Marley and Jane both run a 200m race. If Jane is 1.2 times as fast as Marley, and it takes Jane 21 seconds to complete the race, how long does it take Marley?
Let “M” represent Marley’s speed. Remember that if d = rt, then r = d/t. Jane’s rate of speed therefore is 200/21.
Since Jane is 1.2 times as fast as Marley, 200/21 is 1.2 times Marley’s speed: 200/21 = 1.2M
Solve for M:
200/(21 ⋅ 1.2) = M
200/(25.2) = M
Recall that this is in d/t format. Therefore, it takes Marley 25.2 seconds to run the 200m race.
Additional resources:
Once upon a time mathematicians realized you couldn't take the square root of a negative number. This was a total bummer because that left a lot of problems unsolved. But then Girolamo Cardano was like, "Bro, look, we can do this thing and it will work." And René Descartes said, "What are you going to do, make something up? Oooh look at my 'iMaGiNaRy' numbers." But Cardano was just like "Yep." And Descartes was like, "... Okay fine, I'll go with it but I'm not happy about it," and now we have the imaginary unit.*
*Some liberties were taken in the writing of this historical account. But if you're interested in the full story, visit the SSC library to learn more!
The imaginary unit, denoted by the lowercase letter "i," is equal to the square root of negative 1. It was initially a theoretical concept, considered "imaginary" because no real number could be squared to result in a negative number. However, it became crucial for solving certain polynomial equations and formed the basis for the development of complex numbers.
i2 = -1
i3 = -i
i4 = 1
To simplify ix determine the closest value less than or equal to x that is divisible by 4. Perform the division and focus on the remainder:
- If the remainder is 3 then the solution is –i;
- if the remainder is 2 then the solution is –1;
- if the remainder is 1 then the solution is i;
- if the remainder is 0 then the solution is 1
Note: when simplifying the square root of a negative number, always start by “pulling out the i".
Click image to enlarge.
(a + bi) - (c +di) = (a - c) + (b - d)i
(a + bi)(c +di) = (ac - bd) + (ad + bc)i
(a + bi)(a - bi) = a2 + b2
CH 1.3 EXAMPLES:
Simplify the following:
- √(-4)
- √(-12)
- (2 + 3i) - (3 – 5i)
- i97
SOLUTIONS:
- √(-4) = i√(4) = 2i
- √(-12) = i√(12) = i√(4)√(3) = 2i√(3)
- (2 + 3i) - (3 – 5i) = -1 + 8i
- i97 = i96i1 = i
Additional resources:
"There is nothing in the world quite so satisfying as a quadratic equation." — said somebody, probably, at some point.
The zero-factor property states that if ab = 0 then a or b or both = 0.
The square root property states that the solution set of x2 = k is ±√k
There are three main methods to solve quadratic equations:
- Factoring: This method involves rewriting the quadratic expression as a product of two linear expressions. Does not work if the quadratic equation isn’t easily factorable. Note the following generic patterns:
- ax² + bx + c = 0 -----> (x + ?)(x + ?) All terms positive.
- ax² - bx - c = 0 -----> (x - ?)(x + ?) When all terms are negative, one factor will be negative, and one will be positive.
- ax² + bx - c = 0 -----> (x + ?)(x - ?) When b is positive and c is negative, one factor will be positive and the other will be negative.
- ax² - bx + c = 0 -----> (x - ?)(x - ?) When b is negative and c is positive, both factors will be negative
- Completing the Square: This method involves manipulating the quadratic equation to create a perfect square trinomial on one side. This method will always work.
- Quadratic Formula: This formula provides a direct solution for any quadratic equation in the form ax² + bx + c = 0. This method will always work.
Rationalizing the denominator means rewriting a fraction so that the denominator is a rational number, meaning it doesn't contain any radicals. Though a denominator can be complex, it is common to want to avoid complex numbers in the denominator. You can then simplify the fraction to remove "i" from the denominator by multiplying the numerator and denominator by the complex conjugate of the denominator.

When using the quadratic formula, the discriminant (b2 - 4ac) indicates how many solutions and what type. See the table below:
|
Solutions of a Quadratic Equations |
||
|
Discriminant (b2 - 4ac) |
Number of Solutions |
Type of Solution(s) |
|
Positive perfect square |
Two |
Rational |
|
Positive but not a perfect square |
Two |
Irrational |
|
0 |
One, multiplicity 2 |
Rational |
|
Negative |
Two |
Complex |
The multiplicity of a root (also known as a zero) of a polynomial is the number of times the corresponding factor appears in the factored form of the polynomial. For example, in the polynomial (x - 2)3 (x + 1)2, the root x = 2 has a multiplicity of 3, and the root x = -1 has a multiplicity of 2. This will be discussed more in chapter 3.
Additional resources:
You weren't expecting geometry, were you?
Where "a" and "b" are the legs and "c" is the hypotenuse of a right triangle.
If a projectile is launched vertically upward from height “c” with an initial velocity of “b” the height, x, after “t” seconds can be modeled by the following equation:
x = -16t2 + bt + c
Note: many students wonder where the “-16” comes from in this equation. According to legend, Galileo Galilei dropped different objects of varying weights off of the Leaning Tower of Pisa and developed the formula d = 16t2 for the distance a free falling object travels after “t” seconds, neglecting air resistance and regardless of the object’s weight. Legend or not, this formula works. This concept is covered more in physics!
Additional resources:
Is that boss level music?
- Rational equations that simplify to linear equations or quadratic equations.
- Be sure to check your proposed solution(s)! Remember that division by 0 is undefined.
- Work Rate.
- If 1 job can be completed in "t" time, then the rate of work is r = 1/t
PARTS OF A RADICAL:

Additional resources:
Things don't always balance out. But it's okay, we have math for that.
Important!
When multiplying or dividing both sides of an inequality by a negative you must reverse the inequality symbol.
Additional resources:
This is the |absolute| best. Ba dum tss.
| Absolute value equation or inequality where k ≠ 0 | Equivalent form | Solution set |
| |x| = k | x = k or x = -k | {-k, k} |
| |x| < k | -k < x < k | (-k, k) |
| |x| > k | x < -k or x > k | (-∞, -k) ∪ (k, ∞) |
Chapter 2: Graphs and Functions
Welcome to the GPS of math—functions tell you where you're going, and graphs show you all the weird turns you took to get there. Use the numbered tabs above to find helpful notes, formulas, and additional resources for each section of this chapter.
The mathematical way to know exactly where you are.


No dysfunctional relationships here, no way...
The domain is the set of all the independent variables, x.
The range is the set of all the dependent variables, y.
I really have nothing pithy to say about this.
f(x) = ax + b
If a ≠ 0, then the domain and the range of f are both (-∞, ∞)
Note: "f(x)" is read as "f of x".

Note: the slope of a vertical line is undefined. The slope of a horizontal line is 0.
You probably thought this chapter couldn't possibly get more exciting but oh ho ho...you might be right.
Standard form: Ax + By = C
Slope-intercept form: y = mx +b
Equation of a vertical line through the point (a,b): x = a
Equation of a horizontal line through the point (a,b): y = b
Two lines, neither of which is vertical, are perpendicular if and only if the product of their slopes is -1.
Chapter 3: Polynomial and Rational Functions
Polynomial and rational functions are like soap operas—polynomials rise and fall dramatically, while rational functions always have a flair for the dramatic exit with sudden breaks and plot twists (a.k.a. asymptotes). Use the numbered tabs above to find helpful notes, formulas, and additional resources for each section of this chapter.
Some models are just so beautiful, am I right?
A parabola ("per-AH-boh-luh") is a U-shaped curve, the graphical representation of a quadratic function, characterized by several key features including:
- Vertex: The point where the parabola changes direction, either reaching a maximum or minimum value. The vertex is represented by the point (h, k). (See "QUADRATIC EQUATION IN VERTEX FORM as well as the additional resources available for this section for more information about "h" and "k".)
- Axis of Symmetry: A vertical line that passes through the vertex and divides the parabola into two symmetrical halves.
- y-intercept: The point where the parabola crosses the y-axis.
- x-intercept: The point(s) where the parabola crosses the x-axis, if it crosses.

Additional resources
Like synthetic cheese.
Additional resources:
Here the zeros are the heroes.
Factor Theorem: For any polynomial f(x) , (x - k) is a factor of the polynomial if and only if f(k) = 0.
Rational Zeros Theorem: If p/q is a rational number written in lowest terms, and ifp/q is a zero of f, a polynomial function with integer coefficients, then p is a factor of the constant term, and q is a factor of the leading coefficient.
Fundamental Theorem of Algebra: Every function defined by a polynomial of degree 1 or ore has at least one complex zero.
Number of Zeros Theorem: A function defined by a polynomial of degree n has at most n distinct zeros.
Conjugate Zeros Theorem: if a polynomial with real coefficients has a complex number as a zero, then its conjugate must also be a zero. In simpler terms, if a + bi is a root of a polynomial with real coefficients, then a - bi must also be a root.
Remainder Theorem: If the polynomial f(x) is divided by (x - k), then the remainder is equal to f(k).
Upper and Lower Bounds:If a polynomial is divided by (x - c) using synthetic division, where 'c' is a positive number, and all the resulting coefficients in the quotient and remainder are non-negative, then 'c' is an upper bound for the real zeros. Conversely, if 'c' is a negative number, and the resulting coefficients alternate in sign (including zero as either positive or negative), then 'c' is a lower bound for the real zeros.
Conjugate Zeros Theorem: If f(x) defines a polynomial function having only real coefficients and if z = a + bi is a zero of f(x), where a and b are real numbers, then the complex conjugate (z̄) is also a zero of f(x).
Bonus: Descartes' Rule of SIgns
Let f(x) define a polynomial function with real coefficients and a nonzero constant term, with terms in descending powers of x.
- The number of positive real zeros of f either equals the number of variations in the sign occurring in the coefficients of f(x), or is less than the number of variations by a positive even integer.
- The number of negative real zeros of f either equals the number of variations in the sign occurring in the coefficients of f(-x), or is less than the number of variations by a positive even integer
Additional resources:
- Intro to Zeros (video)
- Rational Zero Theorem Tested (video)
- Finding All the Zeros of a Polynomial (video)
- Finding Zeros of Polynomial Functions (article)
- Online Zeros Calculator (calculator)
Chapter 4: Inverse, Exponential, and Logarithmic Functions
Inverse, exponential, and logarithmic functions are like the sitcom trio of math—one undoes what the other does, one grows way too fast, and the last one helps you figure out what on earth just happened. Use the numbered tabs above to find helpful notes, formulas, and additional resources for each section of this chapter.
I bet your excitement is like f(x) = ax where a < 0.

An exponential function calculates the exponential growth or decay of data. The basic exponential function is f(x) = ax, where x is the input variable as an exponent, and a is a positive number greater than 1.
Note: Exponential functions are useful for modeling real-world phenomena like populations, radioactive decay, interest rates, and the amount of medicine in the bloodstream!
CHARACTERISTICS OF THE GRAPH f(x) = ax |
| The points (-1, 1/a) and (0,1) and (1,a) are on the graph. |
|
If a is greater than 1, then f is an increasing function. On the other hand, if a is less than 1 but greater than 0, f is a decreasing function. a > 0 → increasing 0 < a < 1 → decreasing |
| The x-axis is the horizontal asymptote. |
| The domain is (-∞, ∞), and the range is (0, ∞) |
The word "logarithm" originates from the Greek words "logos" (meaning "proportion" or "ratio") and "arithmos" (meaning "number"). John Napier coined the term in the early 17th century. So now we both know.
Logarithms are a way of writing and working with the exponents. A logarithm is the power to which a number must be raised in order to get some other number For example log3 9= 2, because 3 must be raised to the power of 2 to in order to equal 9.
If a > 0, a ≠ 1, and x > 1 then the logarithmic function with base a is as follows:
Logax = n
Read as "Log base a of x equals n."
Where "a" is the base, "x" is the argument (also called the answer), and "n" is the exponent.
The following table shows several pairs of equivalent statements:
| EXPONENTIAL FORM | LOGARITHMIC FORM |
| 23 = 8 | log28 = 3 |
| 102 = 100 | log10100 = 2 |
| 51 = 5 | log55 = 1 |
| 3-2 = 1/9 | log31/9= -2 |
| 0.5-4 = 16 | log0.516 = -4 |
CHARACTERISTICS OF THE GRAPH f(x) = logax |
| The points (1/a, -1), (1,0) and (a,1) are on the graph. |
|
If a is greater than 1, then f is an increasing function. On the other hand, if a is less than 1 but greater than 0, f is a decreasing function. a > 0 → increasing 0 < a < 1 → decreasing |
| The y-axis is a vertical asymptote. |
| The domain is (0, ∞), and the range is (-∞, ∞) |
Properties of Logarithms
For x > 0, y > 0, a > 0, a ≠ 1, and "r" is any real number:
- PRODUCT PROPERTY: logaxy = logax + logay
- QUOTIENT PROPERTY: logax/y = logax - logay
- POWER PROPERTY: logaxr = r logax
- LOGARITHM OF 1: loga1 = 0
- BASE a OF LOGARITHM a: logaa = 1
Theorem on Inverses
For a > 0, a ≠ 1, the following properties hold:
alogax = x (for x > 0) and logaax = x
Additional resources:
Ah yes, look at this field of fresh, natural logarithms, just about ripe for the harvest.
The two most important bases for logarithms are base 10 and base e. Base 10 logarithms are called common logarithms. The common logarithm of x is written log x where the base is understood to be 10. Basically, is you seem something like log 2 or log 9, it is implied that the base is 10.
log x = log10x
Logarithms with base e are called natural logarithms and are written as ln x (pronounced "L n x" or "El-en x"). They're called natural logarithms because they occur in natural situations that involve growth or decay.
ln x = lnex
Recall that "e" represents a fundamental constant, often referred to as Euler's number, and is approximately equal to 2.71828. It's the limit of the expression (1 + 1/n)n as n approaches infinity. (You'll learn more about limits if you study calculus.)
Many calculators only have log and ln built in, making logarithms with other bases difficult to calculate. However, the change of base theorem is useful for evaluating logarithms where the base is something other than 10 or e. For any positive, real numbers x, a, and b where neither a nor b = 1, the following is true:
For example, to calculate log721 you can use the change of base theorem and compute the following:
This is just like the last section except different.
Property of Logarithms:
If x > 0, y > 0, a > 0, and a ≠ 1, then the following holds:
x = y is equivalent to logax = logay
Additional resources:
After finishing this section, please go back and laugh at my 4.2 joke.
In many situations in ecology, biology, economics, and the social sciences, a quantity (y) changes at a rate proportional to the amount present (y0). The amount present at time t is a special function of t called an exponential growth or decay function:
Let y0 be the amount or number present at time t = 0. Then, under certain conditions, the amount y present at any time t is modeled by
y = y0ekt, where k is a constant
The constant k determines the type of function. When k > 0, the function describes growth. When k < 0, the function describes decay.
Chapter 5: Systems and Matrices
What if, instead of solving one equation at a time, you got to solve two equations at the same time. Eh? Fun, right? Use the numbered tabs above to find helpful notes, formulas, and additional resources for each section of this chapter.

A system of linear equations is a set of two or more linear equations that involve the same variables. For example 2x + 3y = 15 and x - 2y = 7 are both linear equations with two variables (x and y). When considered together, they form a system of linear equations.
- Read the problem carefully until you understand what is given and what is to be found.
- Assign variable to represent the unknown values, using diagrams or tables as needed. Write down what each variable represents.
- Write a system of equations that relates the unknowns.
- Solve the system of equations.
- Check the answer in the words of the original problem. Does it make sense?
Additional resources:
Math support FAQ
Our tutoring schedule is always available on our tutoring page. If you have additional questions about how and when you can get math support, please email Karissa.
Not at all! Tutoring is for everyone—whether you're trying to catch up, keep up, or level up.
Math tutoring at the SSC is walk-in friendly—just stop by during our open hours and a tutor will be happy to help you. You don’t need an appointment! Whether you can only stay for 10 minutes, or 4 hours, drop-in tutoring is here to fit your schedule.
Drop-in tutoring isn’t the same as a study group or a class. You’re welcome to work with friends, but it’s not required. Tutoring takes place in an open space, but your tutor will always give you one-on-one attention.
Tutors won’t lead a session like a teacher would. Instead, they’ll work with you on whatever concepts you need help with—at your pace and level. Since drop-in tutoring is student-driven, be sure to bring questions or topics you’d like to go over!
If you can't make it in person, you can also email us with questions or to connect with a tutor. And don’t forget—our website has a collection of helpful online resources, including videos, guides, and practice tools you can use anytime.
Your tutor will answer any questions, explain tricky concepts, help with practice problems, review assignments, and build your confidence. You won’t just get answers—you’ll learn how to find them.
Yes! While they won’t do your work for you, tutors can walk you through similar problems and show you strategies to tackle questions on your own.
That’s exactly why we’re here. Our tutors create a judgment-free zone where questions are always welcome, and mistakes are part of the process.
Take a deep breath—the Student Success Commons is here to help! Whether you're stuck on a math problem, stressed about a class, or just feeling overwhelmed, you don’t have to figure it all out on your own. Please email the SSC. Please include any information you think will help, such as your class and concerns, to ensure you're connected with the right resource for you.
| SYMBOL | MEANING |
|---|---|
| x | Most commonly used variable, represents an unknown value |
| ≠ | Not equal to, does not equal |
| ≈ | Approximately equal to |
| > | Greater than |
| < | Less than |
| ≥ | Greater than or equal to |
| ≤ | Less than or equal to |
| () | Parentheses |
| [] | Brackets |
| {} | Braces |
| ± | Plus or minus |
| n√a | nth root of a |
| ∅ | Empty set |
| |a| | Absolute value of a |
| | | Such that (used in set builder notation) |
| ∪ | Union ("or") |
| Δ | Uppercase Greek letter "delta", meaning "change in" |
Student Success Commons at York County Community College112 College Drive Wells, ME 04090
|
Quick links: YCCC Homepage | MyYCCC Portal | Library | YCCC Email | Brightspace | Technical Support